과학과 수학의 불확실성
(1) 확실한 지식? 2020. 3. 3.
(2) 기하학적 사유의 확실성 – 1. 2020. 3. 3.
(3) 기하학적 사유의 확실성 – 2. 2020. 3. 10.
(4) 포르투나와 사피엔티아, 또는 확률적 사유. 2020. 3. 17.
(5) 19세기의 과학과 수학. 2020. 3. 24.
(6) 하이젠베르크의 불확정성 원리. 2020. 3. 31.
(7) 거짓말쟁이의 역설과 양자역학의 서울 해석. 2020. 4. 7.
(8) 수학기초론과 괴델의 불완전성 정리. 2020. 4. 14.
(9) 인식론의 문제. 2020. 4. 21.
(10) 과학과 수학은 확실한 지식을 주는가? 2020. 4. 21.
김재영 (녹색아카데미).
17세기 유럽의 지식인들에게 피론주의의 문제는 가장 큰 화두였다. 마르틴 루터와 같은 종교개혁주의자에 반대하는 반종교개혁의 근거 중 하나는 피론주의였다. 종교개혁을 내세운 사람들의 중요한 전제는 모든 사람들이 이성적 판단을 통하여 진리에 이를 수 있다는 것이었다. 피론주의에 따르면 이것이 가능하지 않기 때문에 결국 신의 계시와 교회의 가르침에 따르는 것이 옳다는 반종교개혁의 주장이 설득력을 얻게 되는 것이었다.

16세기 후반, 2세기의 탁월한 피론주의자 섹스투스 엠피리쿠스의 『피론주의 개요』와 『교조주의자에 반대함』이 라틴어로 번역되었다. 1620년에 출판된 지안프란체스코 피코의 『헛된 탐구』는 섹스투스 엠피리쿠스의 사상을 토대로 철학 전반에 대한 근본적인 회의주의적 관점을 전개한 저술로서, 당시 유럽 지식인들에게 커다란 반향을 불러일으켰다.
또한 인간이 올바른 지식을 결코 얻을 수 없으며 모든 분야의 지식을 의심할 수밖에 없기 때문에 관습과 종교적 규율에 따라 사는 것이 가장 행복한 것임을 주장한 미셸 몽테뉴의 사상은 17세기 프랑스에서 지대한 영향을 미치고 있었다.
이런 지적 풍토에서 데카르트도 피론주의의 문제를 피해갈 수는 없었고, 그가 방법적 회의를 통해 찾아낸 것은 바로 그렇게 회의하고 있는 자신의 존재였다. 사악한 존재가 내가 세상에서 보고 판단하는 모든 것을 방해해서 잘못된 것을 올바른 것으로 믿게 만들지도 모르지만, 그렇게 의심하고 있는 내가 존재한다는 것은 흔들리지 않는 진리라는 것이다.
그런 의미에서 데카르트의 말은 “나는 의심하기 때문에 존재한다.”(dubito ergo sum)라고 표현하는 것이 더 올바를 것이다. 의심하는 자신의 존재가 확실하다는 점으로부터 신의 확실함과 수학적 물리학의 확실함으로 나아가는 것은 데카르트에게 자명한 논리였다.

스피노자의 『에티카』 즉 윤리학이 “기하학적 질서에 따라 증명된”(Ordine geometrico demonstrata)이라는 부제를 달고 있는 것도 마찬가지 맥락에서 이해할 수 있다. 현대의 관점에서 보면 윤리 또는 도덕을 기하학적 질서에 따라 증명한다는 것이 낯설지만, 여기에서 기하학적 질서란 다름 아니라 확실한 지식의 표본을 따라간다는 의미이다. 자신이 전개하는 주장들이 확실한 지식임을 보이기 위해서 기하학적 질서를 따랐다는 것이다.
스피노자가 표준으로 삼았던 기하학적 질서의 모범은 에우클레이데스의 기하학이었다. 모두 13권으로 이루어진 에우클레이데스의 『원론』(스토이케이아)은 특이한 구성을 보여준다. 5개의 공리와 10개의 무정의용어로 이루어진 15개의 공준이 있고, 이로부터 엄격한 연역적 논증을 통해 465개의 정리들을 증명하는 형식으로 이루어져 있다.

정리로 제시된 주장들은 미리 주어진 공준을 받아들이는 한 확실하게 증명할 수 있는 지식이다. 즉 사람들이 충분히 수용할 수 있는 공준을 우선 옳다고 인정한다면 거기에서 유도되는 정리들은 그 참됨을 의심할 필요가 없는 옳은 지식이 되는 것이다. 이와 같은 지식체계의 구성을 공리계적 구성이라 한다.
기하학적 지식의 확실성은 이후 수학의 확실성으로 이어졌다. 우리가 대표적인 과학이론이라고 생각하는 뉴턴의 역학체계는 『자연철학의 수학적 원리』라는 제목의 논저에서 제시되었다. 이 책은 흔히 ‘프린키피아’로 약칭된다. 뉴턴의 접근이 강력한 힘을 발휘하게 되는 것은 그 논리적 전개가 기하학의 방법으로 이루어져 있기 때문이다.
『자연철학의 수학적 원리』는 기하학적 구성으로 서술되어 있다. 공리에 해당하는 운동의 법칙(axiomata)이 세 개로 제시되어 있고, 필요할 때마다 그 책에서 각 용어들이 어떤 의미로 정의되는지 명확하게 밝혀 놓았다.
주장들은 모두 명제의 형식으로 되어 있으며, 주장의 성격에 따라 예비정리(lemma), 따름정리(corollary), 명제(proposition)라는 이름이 붙어있다. 예를 들어 [그림 4]는 케플러의 둘째 법칙에 해당하는 내용이 담긴 페이지인데, 그 정리는 공리와 정의들로부터 기하학적인 연역과정을 통해 증명된다.

『자연철학의 수학적 원리』가 이미 알려져 있는 법칙이나 주장들을 연역적 증명으로 확인하는 데 그쳤더라면, 뉴턴의 영향력이 그렇게까지 커지지는 않았을 것이다. 뉴턴의 이론은 구체적이면서도 설명하기 힘든 현상에 아주 잘 맞아떨어졌다.
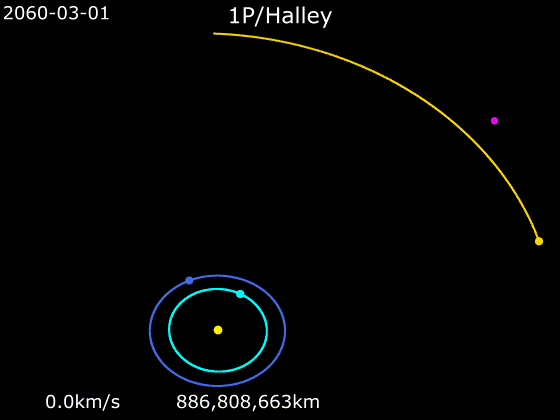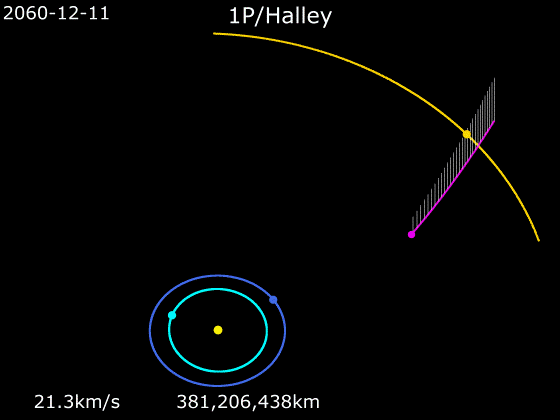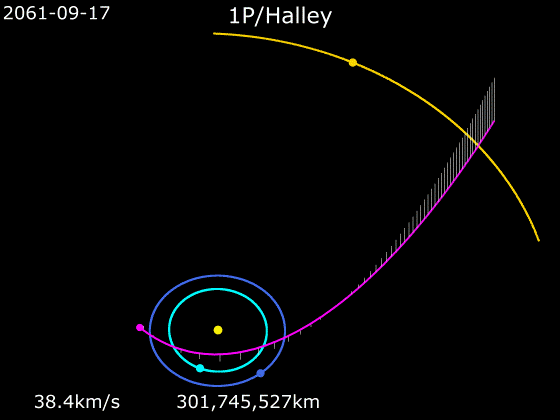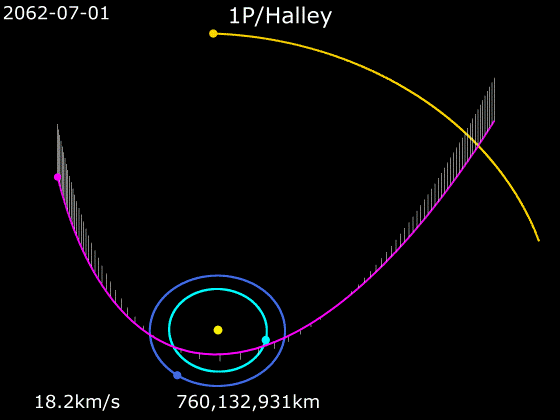
가령 영국의 제2대 왕실천문학자 에드먼드 핼리는 『혜성천문학 개요』(1705)에서 자신이 1682년에 관측한 혜성이 1305년, 1380년, 1456년, 1531년, 1607년에 나타난 혜성과 같은 것이며, 1758년에 다시 나타날 것이라고 예측했다.
이 주장은 10여 년 동안 혜성의 궤도와 운동을 연구한 결과였으며, 뉴턴의 이론을 기반으로 한 것이었다. 혜성이 한번 지구를 스쳐 지나가는 것이 아니라 아주 많이 찌그러져 있긴 해도 타원 모양의 궤적을 그린다고 핼리가 믿은 까닭은 정교한 기하학적 증명으로 뒷받침된 뉴턴의 이론이 있었기 때문이었다.
핼리가 세상을 떠난 뒤 16년 만에 모습을 다시 드러낸 그 혜성을 핼리 혜성이라고 부르게 된 것은 자연스러운 일이다. 핼리는 고대 바빌로니아의 기록을 원용하여 일식과 월식의 주기에 사로스 주기라는 이름을 붙인 것으로도 유명하다. 사로스 주기 6585.3일, 즉 18년 11일 8시간이 지나면, 지구와 태양과 달의 배치가 원래와 거의 같아진다. 사로스 주기만으로도 일식이나 월식의 정확한 예측이 가능하다.
혜성과 일실 및 월식에 대한 핼리의 확실하고 틀림없는 계산은 19세기 동안 더 정교해지고 더 체계적으로 발전했다. 피에르-시몽 라플라스의 다음과 같은 언급은 세계를 이해하는 데에 이 기하학적 토대의 물리학이 얼마나 확실한 지식을 줄 수 있는가에 대한 자신감을 잘 보여준다.
“주어진 특정 순간에 자연을 움직이는 모든 힘과 자연을 이루는 존재들의 각각의 상황을 다 알고 있는 어떤 지성이 이 모든 정보를 다 분석할 수 있을 만큼 뛰어나다면, 이 지성은 우주의 거대한 천체들로부터 가장 작은 원자에 이르기까지 그 운동을 같은 공식으로 포괄할 수 있을 것이며, 과거와 현재와 미래의 그 어떤 것도 불확실한 것은 없을 것이다.”
피에르-시몽 라플라스
이를 더 명료하게 말하면, 물질의 상태를 특정 순간의 위치와 운동량의 값으로 정해준다고 할 때, 특정 시간의 상태로부터 임의의 다른 시간에 물질의 위치와 운동량의 값이 어떻게 주어질지에 대해 정확히 예측할 수 있다는 것이다.
그러나 동시에 라플라스의 언명은 넓은 의미에서는 언젠가 모든 자연법칙을 알아내고 이를 적용하는 방법까지도 밝혀냄으로써 물질세계에 대해 모든 것을 알 수 있으리라는 물리학자들의 강력한 희망을 피력하고 있는 것이기도 하다. 이는 고전역학적 세계관에서 나타나는 물리학자의 자신감이다.
라플라스 자신은 19세기 천문학에서 가장 권위 있는 저서였던 『천체역학』 다섯 권의 저자였다. 1799년부터 1825년까지 저술된 이 책은 기하학으로 서술되고 증명된 뉴턴의 역학체계를 미적분학으로 다시 쓴 역작이기도 했지만, 동시에 천체현상에 대한 매우 정교한 계산을 집대성한 요약이기도 했다.
사실 이 다섯 권의 책에는 라플라스 자신의 고유한 업적보다는 당시까지의 많은 뛰어난 사람들이 이루어낸 것이 따로 언급되지 않은 채 포함된 경우가 많기 때문에 라플라스의 학문적 도덕성이 의심되기도 한다. 그렇긴 하지만 『천체역학』이 상징하는 확실한 지식은 19세기 유럽에서 중요한 이정표였다.
(4) 포르투나와 사피엔티아, 또는 확율적 사유(2020. 3. 17.)로 이어집니다.
과학칼럼은 매주 화요일 업로드 됩니다.
참고문헌
- 김재영. (2001). “한계로서의 확률: 양자역학과 통계역학의 예”, 『과학과 철학』, 제12집. pp. 1~20.
- 김재영. (2004). “통계역학의 기초 다시 보기: 메타동역학적 접근”, 『과학철학』, 제7권 pp. 21~63.
- 김재영. (2010). “불확실성의 과학은 어떻게 만들어졌는가?”. 박성민 외, 『불확실한 세상』 사이언스북스. pp. 251-284.
- 야마오카 에쓰로 (2004). 『거짓말쟁이의 역설』, 안소현 옮김, 영림카디널.
- 장회익 외 (2016). 『양자, 정보, 생명』 한울아카데미.
- Franzén, Torkel (2005). Gödel’s Theorem. An Incomplete Guide to Its Use and Abuse. A K Peters.
- Gigerenzer, G. et al. (1989). The Empire of Chance: How probability changed science and everyday life. Cambridge University Press.
- Goldstein, R. (2005). Incompleteness: The proof and paradox of Kurt Gödel. Norton; 고중숙. (2007). 『불완전성: 쿠르트 괴델의 증명과 역설』, 승산.
- Hacking, I. (1975). The emergence of probability: A philosophical study of early ideas about probability, induction and statistical inference. Cambridge University Press.
- Harman, P. (19 ). Energy, Force, Matter: Physics in the Nineteenth Century. Harvard University Press; 김동원, 김재영 (2000). 『에너지, 힘, 물질: 19세기의 물리학』, 성우출판사.
- Kline, M. (1982). Mathematics: The Loss of Certainty. Oxford University Press; 심재관. (2007). 『수학의 확실성: 불확실성 시대의 수학』, 사이언스북스.
- 대문사진: 태양계를 지나는 1910년 핼리 혜성. Popular Science magazine, 1910년 그래픽. (출처: wikipedia)

